Variance expliquée

Une corrélation linéaire se traduit par une forme de nuage allongée (ellipse) et traduit (entre autre) le fait que l'on peut prédire le score observé sur une variable si on connaît le score observé sur l'autre variable avec moins de chance de se tromper que si on ne le connaissait pas (ce qui traduit la co-variation ou la co-dépendance entre les mesures) .  

Par exemple, lorsqu’aucune information n’est disponible sur une variable, la meilleure estimation possible pour une nouvelle observation correspond à la moyenne des valeurs observées de cette variable. Le risque d’erreur associé à cette prédiction est d’autant plus élevé que la variance des observations de A est importante. Ainsi, l’intervalle de confiance lié à cette estimation dépend directement de la variance de A. En revanche, si l’on connaît la corrélation entre A et une autre variable B, et que la valeur de B est disponible pour la nouvelle observation, la prédiction de A peut être affinée. Elle tient alors compte de la relation entre les deux variables, ce qui permet de réduire la part de variance non expliquée. La prédiction devient ainsi plus précise, et la probabilité d’erreur diminue d’autant plus que la corrélation entre A et B est forte.

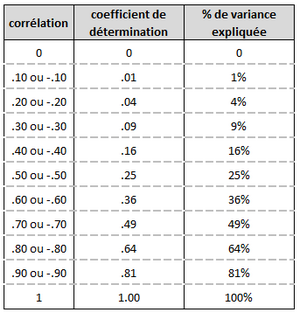
En fait, lorsque deux tests corrèlent, cela signifie qu'une partie de la variance de chacun des tests est "expliquée" par la variance de l'autre test (variance commune), c'est pourquoi l'erreur de pronostic est plus faible. On peut montrer facilement que le pourcentage de la variance expliquée est égal au carré de la corrélation linéaire (r de Bravais Pearson) entre les deux variables multiplié par 100 (le carré de la corrélation linéaire s'appelle le coefficient de détermination). 

Exemples