Certains tests proposent des valeurs seuils ou critiques permettant de définir un risque (difficulté d'apprentissage de la lecture, pronostic de démence, dépression, etc.). Ces valeurs seuils sont parfois fixées a priori à partir de critères comme un score inférieur ou supérieur à 2 écarts-types à celui observé en moyenne. Cependant, quand un test permet de prédire l'apparition d'une maladie ou des difficultés d'apprentissage, il est possible, d'utiliser les notions de sensibilité et spécificité telles que nous les avons vues dans le chapitre (Qualités métrologiques - Sensibilité et spécificité).
Pour rappel la sensibilité dans ce contexte est la capacité de l'instrument à identifier correctement les personnes présentant la caractéristique étudiée et la spécificité est la capacité de l'instrument à identifier correctement les personnes ne portant pas cette caractéristique.
Supposons la construction d'une batterie permettant d'évaluer la mémoire sous toutes ses formes et donnant un score global de mémoire pour les personnes âgées entre 70 et 75 ans qui présentent des plaintes mnésiques (vie quotidienne). L'hypothèse formulée est que les résultats à cette batterie, lorsqu'ils sont élevées (les scores de performances sont inversés), devraient être aussi prédicteurs d'une évolution vers une démence dans les années à venir (exemple fictif). L'épreuve est soumise à un échantillon représentatif de cette population et les résultats sont mis en perspective avec l'évolution des personnes ayant subies ce test. Deux groupes sont constitués : ceux présentant une démence et ceux ne présentant pas de démence. Il est possible de représenter les résultats initiaux à cette batterie sur un graphique en séparant ceux qui présentent un trouble et ceux qui n'en présentent pas :
Figure E.2 : Distribution des scores (proportions) des personnes qui présentent un trouble (T) et de ceux qui n'en présentent pas (NT)
Parmi ceux qui présentent des troubles, le score initial peut être faible (sans difficulté particulière ) et inversement, parmi ceux qui ne présentent pas de trouble, le score initial peut être élevé. Si les deux courbes sont confondues ou presque confondues (moyenne proche) il ne sera pas possible de trouver une valeur critique. Si ces deux courbes sont suffisamment distinctes, il faudra se fixer une valeur critique en minimisant les faux positifs (FP) et les faux négatifs (FN).
Le graphique précédent permet de comprendre que selon la valeur seuil que l'on prendra fixée, soit on diminue la probabilité de FP (faux positifs) mais on augmente la probabilité d'avoir des FN (faux négatifs), soit on diminue la probabilité des FN mais on augmente celle des FP. Le bon positionnement dépend des risques que l'on veut prendre et de la nature de la décision à prendre. Si, comme dans notre exemple, l'objectif est d'avoir une valeur critique pour identifier les personnes à risque de démences, il peut être préférable d'avoir des FN plutôt que des FP connaissant l'impact du diagnostic dans l'évolution de ces maladies. A l'inverse si, pour une autre recherche avec des enfants, l'objet est d'identifier des possibles troubles d'apprentissage ultérieurs (lors de la scolarisation obligatoire), n'est-il pas à préférable de faire un minimum de FN ?
Ce rapport entre FN et FP et la qualité diagnostic de l'épreuve peut être évaluée au moyen d'une courbe que l'on appelle courbe ROC (Receiver Operating Charateristic). Cette courbe permet de montrer à quel point un test arrive à fait correctement la différence entre deux groupes (par exemple, malades et non malades).
Pour tracer cette courbe, on place en abscisse la valeur de 1 - spécificité et en ordonnée la sensibilité (pour le calcul de ces valeurs, voir Qualités métrologiques - Sensibilité et spécificité). Le seuil de décision est progressivement modifié de manière à faire varier la spécificité de 1 à 0. Pour chaque valeur du seuil, le couple de coordonnées (1 – spécificité, sensibilité) est reporté sur le graphique. Cette approche permet ainsi de décrire l’évolution conjointe des faux positifs (FP) et des faux négatifs (FN) en fonction du seuil de décision retenu.
Lorsque la courbe ROC se rapproche de la diagonale, la capacité du test à discriminer entre les deux états (présence ou absence de la condition) diminue, traduisant une classification équivalente à un tirage aléatoire. Dans ce cas, la surface comprise entre la courbe et la diagonale est faible. À l’inverse, un test diagnostique de qualité se caractérise par une courbe ROC située nettement au-dessus de la diagonale, indiquant une meilleure performance discriminante
Le choix du seuil de décision doit être effectué en fonction du compromis acceptable entre la spécificité et la sensibilité, en tenant compte des conséquences associées aux erreurs de classification (faux positifs et faux négatifs). En pratique, le seuil correspondant au point le plus proche de la coordonnée (0,1) est souvent privilégié, car il représente un bon compromis entre la détection correcte des cas positifs et la minimisation des erreurs de classification.
|
Figure G.3 : Exemples de deux courbes ROC. En rouge (pointillé) une courbe ROC associée à un mauvais test diagnostic et en noir (traitillé) une courbe ROC associé à un meilleur test diagnostic (rem : la spécificité et la sensibilité varient entre 0 et 1). |
Pour évaluer la qualité globale des prédictions, il est possible de calculer l'AUC (Area Under the Curve) qui est l'aire sous l'ensemble de la courbe. Les valeurs d'AUC varie de 0 à 1. Un AUC de 0 correspond à un modèle dont 100 % des prédictions sont fausses. A l'inverse, si toutes les prédictions sont correctes, l'AUC est de 1. En règle générale, une AUC comprise entre 0,7 et 0,9 traduit une performance diagnostique satisfaisante ; une AUC supérieure à 0,9 indique une très bonne performance. Une AUC inférieure à 0,5 suggère une inversion du critère de classification (le test classe les cas négatifs comme positifs, et inversement)
Pour calculer cette surface, il existe plusieurs méthodes mais on peut utiliser la formule suivante :
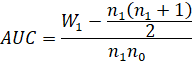
|
W1 : Après avoir classé toutes les observations par ordre croissant, W1 correspond à la somme des rangs des personnes positives. n1 et n0 : ce sont respectivement le nombre de personnes positives et le nombre de personnes négatives. |
Pour aller plus loin
La présentation qui est faite ici des courbes ROC est très simplifiée. Cet outil est très utilisé dans le domaine médical et plus rarement en psychologie. Pour aller un peu plus loin sur la compréhension des courbes ROC, vous pouvez lire un article introductif (Morin, Morin, Mercier, Moineau, & Codet, 1998) dans le domaine médical ou ces articles montrant une application en psychologie (Lacot et al., 2011, Pintea, Moldovan, 2009).