Corrélations partielles

La corrélation observée entre deux variables peut être artificielle (cf. exemple ci-dessous), masquée ou sur-évaluée en raison d'une ou plusieurs variables confondantes. Selon la nature de/des variable(s) confondante(s), la stratégie d'analyse est différente :

-La variable confondante est une échelle d'intervalle.

Le principe est alors de calculer un coefficient de corrélation partielle en retirant la variance qui est due à une troisième variable Z (corrélation partielle entre X et Y notée alors rXY.Z). Cet indice de corrélation partielle permet par exemple de calculer la corrélation entre deux tests après avoir retiré l'effet de l'âge, c'est à dire après avoir retiré la variance des notes due à l'âge des sujets. La formule de calcul est simple :

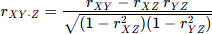
Lorsque qu'il existe plusieurs variables confondantes qui sont des échelles d'intervalles, la corrélation partielle est alors une corrélation partielle d'ordre p (rxy.z1z2...zp) et la formule est alors plus complexe (matricielle). Il est souvent préférable si p est supérieur à 3 de passer par des techniques de régression (non présentée dans ce rappel "statistiques").

-La variable confondante est qualitative

Une variable qualitative ((qui permet de distinguer différents groupes) conduit à calculer la corrélation pour chaque groupe. On peut ainsi avoir des surprises avec par exemple une corrélation négative entre deux variables x et y, qui devient positive pour chacun des groupes (c'est une des expressions du paradoxe de Simpson*, cf. figure B-5) ou encore des corrélations qui varient selon les groupes et qui sont très différentes de celles observées globalement. 

Dans l'exemple donné  (figure B-5) les  scores sur la variable X augmentent avec l'âge et alors qu'ils diminue pour Y avec l'âge. La corrélation entre X et Y est négative (nuage de points orienté vers la gauche). Pour les 4 groupes distingués par la variable Z (4 groupes d'âge correspondant aux 4 couleurs dans le nuage de points), les corrélations entre X et Y sont toutes positives ! Cet effet peut sembler paradoxale mais on doit toujours y penser lorsque l'on regroupe des données de différentes études ou à l'inverse dans les études développementales avec des enfants d'âge très différent.

(*) Le paradoxe de Simpson (ou effet de Yule-Simpson) a été décrit initialement par Udny Yule en 1903 puis repris par Edward Simpson en 1951. De façon générale, cet effet correspond à l'inversion d'un effet (fréquence de guérison, corrélation, etc.) observé dans plusieurs groupes lorsque l'on regroupe toutes les données (par exemple une différence de moyennes entre deux conditions est positive dans un premier  groupe, positive dans le second groupe mais s'inverse quand on combine les deux groupes). Pour ceux qui veulent mieux comprendre ce paradoxe ou voir des exemples surprenants, cf. https://www.youtube.com/watch?time_continue=11&v=vs_Zzf_vL2I