Dans un test cognitif, un item difficile apporte peu d'information (voir aucune information) sur la position d'une personne qui présenterait des difficultés (position basse sur le trait latent mesuré) et inversement un item facile apporte peu d'information concernant une personne qui aurait, sur ce même trait latent une valeur élevée. Selon le paramètre de difficulté, un item permettra de différencier plus ou moins les élèves en fonction de leur position sur le trait latent. Cet exemple concernant le paramètre de difficulté est une façon d'illustrer le fait que chaque item apporte une information différente selon la valeur que prend θ (trait latent).
On a vu que la courbe caractéristique d'un item associe à chaque valeur de θ (trait latent) la probabilité de réussir cet item. On peut, à partir des paramètres de cette courbe, calculer une courbe qui renseigne sur le "pouvoir" d'information de l'item en fonction des valeurs de θ. Le graphique suivant illustre cette relation entre θ et le niveau d'information apporté par deux items.
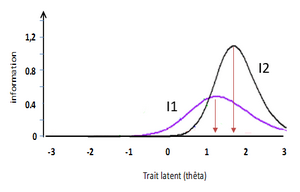
Figure E.9 : Courbe d'information de deux items d'un test (I1 et I2)
Le point haut des courbes renseigne sur le niveau du trait latent pour lequel l'item apportera le plus d'information (sera le plus précis). Dans l'exemple ci-dessus, le pouvoir informatif maximum est observé pour l'item I1 avec une valeur de θ égale à 1.20. Pour I2, le maximum correspond à une valeur de θ égale à 1.75.
Remarques :
■Dans les deux exemples précédents faire passer ces deux items n'apportent aucune information pour des personnes dont la position sur le trait latent serait négative (I1 apporterait en fait très peu d'information et I2, aucune information).
■A partir des courbes d'information des items d'un test, on peut établir la courbe d'information du test qui s'obtient simplement en additionnant les courbes d'information des items (pour chaque valeur de thêta). Cette courbe d'information peut avoir plusieurs points hauts ce qui signifie que le test présente un pouvoir informatif plus important pour différentes valeurs du trait latent.
---------
(*) L'équation qui définit la fonction d'information d'un item est :
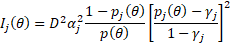
avec : Ij(ϴ)--------Information associée à l'item j au point thêta ϴ--------la valeur du trait latent pj(ϴ)--------la probabilité de répondre à l'item j lorsque la valeur du trait est ϴ αj --------le paramètre de discrimination (égal à 1 pour un modèle à un paramètre) γj --------le paramètre de pseudo chance (égal à 0 pour les modèles à 1 et 2 paramètres) D--------Constante (souvent la valeur utilisée est 1.7) |