On peut représenter graphiquement la relation entre deux mesures par un nuage de points, où l'abscisse d'un point correspond à une échelle de mesure et l'ordonnée à l'autre échelle de mesure. Un individu est donc représenté par un point en fonction de ces scores sur chacune des deux échelles. La représentation d'un ensemble d'individu se traduit par un nuage de points pouvant avoir un axe d'allongement plus ou moins important en relation avec la corrélation linéaire qui existe entre ces deux variables. Le centre du nuage de point correspond au sujet théorique qui aurait pour score la moyenne sur les deux mesures.
Ci-dessous, nous présentons quelques cas typiques de nuages pour différents degrés de corrélation : (1) Corrélation moyenne à forte négative (r = -.60) ; (2) Une corrélation nulle (r = .00) ; (3) Une corrélation forte positive (r = +.93).
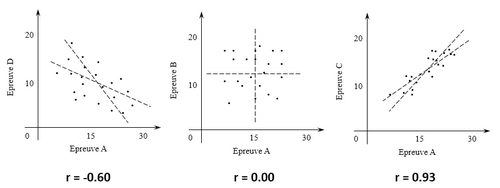
Figure B-3 : Exemples de nuages de points illustrant différents niveaux de corrélations
Remarque
On ne devrait pas calculer de corrélations sans faire d'analyse graphique. C'est un outil privilégié pour visualiser la nature de la relation (linéaire ou non) mais aussi pour repérer des points "déviants" ou "aberrants qui conduisent parfois à créer des relations artificielles. Un exemple extrême est donné ci-dessous montrant la relation entre des notes scolaires en histoire (en abscisse) et en mathématiques (en ordonnée). Dans le premier graphique (figure B-4 gauche) la corrélation calculée est de .60 mais s'explique par un seul point (le point en rouge). En toute logique, ce point aberrant doit être pris en compte dans l'interprétation des données. Ici, il est probable qu'il faut exclure ce point de l'analyse (il s'agit en fait d'une erreur de saisie ou de transformation des notes, les notes étant sur une échelle de 0 à 20). La corrélation corrigée (suppression de ce point) est alors de .32 (ce qui change de façon significative la valeur de la corrélation). On peut aussi avoir des points aberrants qui inversent la corrélation ou l'annulent (cf. l'exemple de gauche ci-dessous). Il s'agit du même nuage de points mais le point aberrant est différent et la corrélation calculée en prenant en compte ce point est de .09 ! La note d'histoire (40) est probablement ici une erreur de saisie. Il faut donc corriger la saisie ou calculer la corrélation sans tenir compte de ce point.
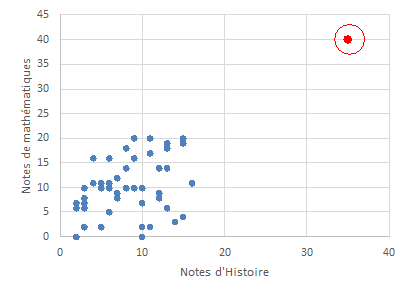
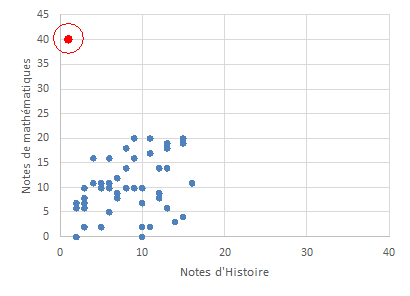
Figure B-4 : Nuages de points identiques traduisant la relation entre les notes observées sur 2 matières (histoire et mathématiques mais avec un point atypique (en rouge et encerclé) différent. |
.